
La sezione Aurea
Matematica nella Natura
1: Definizioni
Cominciamo a parlare della sezione aurea, secondo quanto enunciato nel progetto Matematica nella Natura : il progetto .
La sezione aurea è un concetto antico, molto usato dai Greci della classicità.
La sua definizione originaria è:
Dato un segmento di lunghezza ![]() si definisce la quantità
si definisce la quantità ![]() sezione aurea di
sezione aurea di ![]() se essa è media proporzionale tra l’intero segmento e la sua parte residua.
se essa è media proporzionale tra l’intero segmento e la sua parte residua.
Questa definizione introduce le prime complicazioni.
Cosa vuol dire essere medio proporzionale?
Dobbiamo ricordare cosa è una proporzione.
Dati 4 numeri reali ![]() questi si dicono in proporzione se vale la seguente relazione:
questi si dicono in proporzione se vale la seguente relazione:
![]()
Questa scrittura si legge “a sta a b come c sta a d”.
Nella nostra definizione troviamo la dizione “medio proporzionale”. Esso significa che nella precedente proporzione i due numeri centrali sono uguali, ossia risulta:
![]()
Ciò premesso la relazione che definisce la sezione aurea è la seguente:
![]()
Si tratta di quella che viene detta “proporzione continua”, ma per la sua risoluzione si procede tramite una equazione di secondo grado.
2: Significato della proporzione
Prima di procedere vogliamo però fare un passo indietro: cosa significa essere in proporzione?
Intuitivamente due coppie di quantità, numeri nel caso di una impostazione algebrica, sono tra loro in proporzione se la prima e la seconda coppia hanno lo stesso rapporto. Ancora più informalmente la proporzionalità rappresenta bene il concetto di “fotocopia” ingrandita oppure rimpicciolita. Si parla propriamente di fattore di scala introdotto dalla proporzione.
Facciamo un esempio numerico per chiarirsi le idee: i numeri 15, 10, 180, 120 sono tra loro in proporzione.
In effetti la seconda coppia è la “fotocopia ingrandita” sei volte della prima. Ovviamente il fattore 6 è casuale, si poteva scegliere un qualunque numero. Ad esempio ![]() potrebbe essere un fattore di scale che “rimpicciolisce” l originaria frazione
potrebbe essere un fattore di scale che “rimpicciolisce” l originaria frazione ![]() .
.
Infatti a titolo di cronaca entrambe le coppie hanno rapporto ![]() . In genere questo rapporto viene espresso in forma di frazione irriducibile oppure, quando possibile, come numero intero.
. In genere questo rapporto viene espresso in forma di frazione irriducibile oppure, quando possibile, come numero intero.
La regola pratica per la soluzione della proporzione ![]() è semplice e deriva da una constatazione.
è semplice e deriva da una constatazione.
I numeri ![]() sono uguali sempre per i numeri in proporzione.
sono uguali sempre per i numeri in proporzione.
Di conseguenza conoscendo 3 numeri dei 4 si può calcolare quello mancante, usualmente indicato con la lettera ![]() .
.
Ad esempio se abbiamo i numeri ![]() possiamo scrivere esplicitamente la proporzione:
possiamo scrivere esplicitamente la proporzione:
![]()
Avendo notato che deve valere l’uguaglianza della coppia di prodotti ![]() il valore incognito
il valore incognito ![]() è facilmente calcolabile come
è facilmente calcolabile come ![]() quindi infine:
quindi infine:
![]()
Chiaramente questo è solo un caso particolare, cambiando i numeri e la posizione della incognita ![]() si ottengono valori diversi per la proporzione.
si ottengono valori diversi per la proporzione.
Altri esempi sono:
![]()
![]()
![]()
con i numeri decimali:
![]()
![]()
![]()
Sono esempi di proporzione continua le seguenti:
![]()
![]() .
.
Nelle proporzioni continue la determinazione della incognita ![]() è legata alla estrazione della radice quadrata del prodotto degli altri termini numerici noti.
è legata alla estrazione della radice quadrata del prodotto degli altri termini numerici noti.
Per chi fosse interessato alle proprietà analitiche ulteriori si può notare che la soluzione della proporzione continua è la media geometrica dei due numeri che compaiono nella proporzione.
Nel caso della prima proporzione il calcolo è questo:
![]() .
.
Per la seconda proporzione continua proposta le cose si complicano, infatti il prodotto di 7 e 5, ossia 35, non è un quadrato perfetto.
Si deve quindi estrarre una radice quadrata oppure non fornire un risultato approssimato lasciando la radice in forma esatta.
Si ottiene quindi ![]() oppure in forma esatta
oppure in forma esatta ![]() .
.
Chiaramente quanto riportato è solo una piccola parte delle definizioni e proprietà delle proporzioni. Per approfondire si può ricorrere ad un qualunque libro di aritmetica oppure al web: vedasi Wikipedia.
Con queste premesse possiamo affrontare la proporzione che definisce il rapporto aureo:
3: Soluzione della proporzione aurea
Abbiamo visto come si possono risolvere le proporzioni continue, ma la proporzione aurea è più complessa. Si deve ricorrere alla risoluzione di una equazione di secondo grado.
Presa la ![]() dobbiamo elaborare la proporzione sfruttando l’uguaglianza di rapporti.
dobbiamo elaborare la proporzione sfruttando l’uguaglianza di rapporti.
Riscriviamo in questo modo: ![]()
Dando per scontato che i denominatori di questa relazione siano non nulli si ottiene:
![]()
Ricordiamo che avere i denominatori nulli equivale a dividere per zero. E in tutta la Matematica la regola assoluta è che non è consentito dividere per zero.
Applicando le usuali regole di calcolo il primo membro dell’equazione si trasforma ottenendo
![]()
dopo aver svolto la moltiplicazione.
Quindi raccogliendo tutto al secondo membro uguagliato a zero:
![]()
ricordiamo che la nostra quantità incognita è ![]() , mentre quella nota è
, mentre quella nota è ![]() .
.
Di conseguenza è necessario risolvere l’equazione nella variabile ![]() .
.
A questo punto applichiamo la regola di risoluzione delle equazioni di secondo grado e risolviamo. Per chi non conoscesse, o non ricordasse, la suddetta formula nel successivo paragrafo 5 diamo dei cenni per comprendere il procedimento.
Ebbene le due soluzioni dell’equazione data sono:
![]()
![]()
La prima soluzione conduce ad una valore di ![]() negativo in relazione al valore di
negativo in relazione al valore di ![]() , è quindi inaccettabile cercando noi un valore relativo ad una lunghezza.
, è quindi inaccettabile cercando noi un valore relativo ad una lunghezza.
La seconda soluzione conduce invece ad un valore positivo e come tale lo considereremo come unico accettabile indicandolo semplicemente ![]() in luogo del precedente
in luogo del precedente ![]() .
.
Tale valore è irrazionale e ha un valore approssimato di ![]() .
.
Se volete approfondire la parte analitica potete trovare alcune note nella parte 5.
4: La sezione aurea nell’arte e sue proprietà
Per prima cosa notiamo che da sempre il rapporto aureo ha colpito la mente di civiltà antiche che hanno attribuito ad esso una valore estetico particolare.
Ad esempio alcune delle lunghezze del Partenone di Atene in Grecia sono tra loro in sezione aurea.
Dopo averla calcolata la sezione aurea vediamo quali siano le sue proprietà analitiche.
Come detto in precedenza consideriamo il valore della sezione aurea positivo. Ignoriamo quello negativo perché nella geometria usuale non può rappresentare una lunghezza.
Ci concentreremo quindi sul valore ![]() avendo avuto cura di considerare come unitario il valore del segmento di partenza, ossia ponendo
avendo avuto cura di considerare come unitario il valore del segmento di partenza, ossia ponendo ![]() .
.
Con questa scelta consideriamo la parte aurea della misura unitaria, ossia svincolata da ogni specifica misura e valida come percentuale. Per chi se la ricorda la stessa cosa viene fatta in Trigonometria.
La prima proprietà della sezione aurea è quella implicita nella definizione stessa della proporzione continua:
![]()
Il rapporto al primo membro, tra la sezione aurea dell’unità e la sua parte residua prende il nome di rapporto aureo.
Chiariamo subito una cosa: parlando di rapporto aureo abbiamo reso inutile considerare la lunghezza del segmento iniziale. Ecco perché abbiamo in questo paragrafo detto che possiamo ignorare il valore della lunghezza e riferirci alla sola lunghezza unitaria.
Ma quanto vale il rapporto aureo? Calcoliamolo partendo da ![]() .
.
![]()
Di conseguenza il rapporto aureo, generalmente indicato con la lettera greca ![]() (tradotta in italiano come “fi”),assume la forma:
(tradotta in italiano come “fi”),assume la forma:
![]()
Ancora non ci siamo, facciamo alcune semplificazioni ottenendo:
![]()
Dobbiamo ancora procedere, eseguendo quella operazione che i matematici chiamano razionalizzazione del denominatore :
![]()
![]()
si arriva infine a:
![]() .
.
Questo è il rapporto aureo.
Se vogliamo dare a lui una valutazione approssimata otteniamo:
![]() .
.
Concludiamo con una considerazione: la particolarità della sezione aurea e del relativo rapporto è implicita anche nella proporzione che abbiamo riscritto poc’anzi.
Infatti abbiamo elaborato il rapporto aureo dal primo membro, ma questo valore, in virtù dell’uguaglianza, è lo stesso al secondo membro.
Ossia ritroviamo il rapporto aureo come reciproco del valore della sezione aurea.
Abbiamo fatto una escursione su un argomento di matematica che cavalca i secoli. E abbiamo notato che è effettivamente un numero ricco di proprietà.
Cosa c’entra con la natura?
Abbiate un attimo di pazienza, il legame con la malacologia verrà chiarito nei prossimi articoli.
Per approfondire vedi la voce sulla Enciclopedia britannica relativa all’argomento.
La lettura di questo articolo, piuttosto lungo, è conclusa se non siete interessati ai dettagli matematici.
Se, al contrario, volete rinfrescare alcuni concetti citati, le equazioni di secondo grado, continuate la lettura con la prossima sezione.
5: Ricordiamo le equazioni di secondo grado
Abbiamo ricordato nei paragrafi precedenti la necessità di risolvere una equazione di secondo grado.
Vogliamo richiamare, in maniera molto veloce e semplice, come risolvere in modo generale una equazione di secondo grado.
Per prima cosa che cosa è una equazione in una incognita?
L’equazione in una incognita è una espressione che dipende da un valore incognito, usualmente indicato con ![]() uguagliata ad una altra espressione oppure ad un numero.
uguagliata ad una altra espressione oppure ad un numero.
L’uguaglianza proposta si concretizza solo per un valore dell’incognita.
Le equazioni in una incognita più semplici sono quelle di primo grado.
Generalmente le equazioni di primo grado, dette anche equazioni lineari, hanno una forma generale del tipo: ![]() , detta anche forma canonica.
, detta anche forma canonica.
Ossia l’incognita moltiplicata per un valore numerico e un termine noto uguagliate a zero.
Facciamo un esempio numerico: ![]() . Tale esempio è la forma generale.
. Tale esempio è la forma generale.
Ovviamente per giungere alla forma generale si può dover fare molti calcoli. Ma ciò che conta è che una equazione di primo grado è SEMPRE riconducibile alla forma sopra riportata.
Infatti facendo un esempio un minimo più oneroso possiamo scrivere: ![]() . Applicando le regole algebriche (non voglio tediarvi oltre, se vi interessa cercate un libro di Algebra del Liceo Scientifico oppure sulle varie risorse on line) si porta tutto al primo membro:
. Applicando le regole algebriche (non voglio tediarvi oltre, se vi interessa cercate un libro di Algebra del Liceo Scientifico oppure sulle varie risorse on line) si porta tutto al primo membro: ![]() .
.
Quest’ultima conduce a ![]() .
.
Semplificando otteniamo il risultato ![]() . Ricadiamo quindi nella forma canonica che abbiamo visto in precedenza.
. Ricadiamo quindi nella forma canonica che abbiamo visto in precedenza.
Riprendiamo ora la forma canonica con le lettere ![]() e l’esempio particolare
e l’esempio particolare ![]() analizzandoli in parallelo per capire il concetto.
analizzandoli in parallelo per capire il concetto.
Un grafico che rappresenta il nostro esempio è questo:
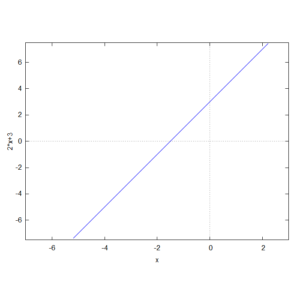
Cosa significa graficamente risolvere l’equazione?
Significa trovare quel valore in cui la linea blu interseca l’asse delle ![]() .
.
Pur non volendo entrare in questo argomento, studiato nella branca della matematica detta Geometria Analitica, notiamo che la dizione di lineare applicata alle equazioni di primo grado è dovuta alla forma di retta che compare quando si disegna graficamente nel piano cartesiano l’equazione al variare dei valori di ![]() .
.
In generale la forma canonica si risolve in via definitiva con il valore:
![]()
quindi nell’esempio proposto con il valore ![]() .
.
Tutto semplice? Beh diciamo di si, le equazioni lineari sono le più semplici da trattare.
Ci sono però delle complicazioni, per cui bisogna avere delle attenzioni (ti pareva che in matematica filasse tutto liscio!).
Cosa succede se uno dei due numeri ![]() oppure
oppure ![]() valgono zero, oppure anche entrambi contemporaneamente?
valgono zero, oppure anche entrambi contemporaneamente?
Le tre ipotesi conducono a risultati molto diversi tra loro.
Caso 1) ![]() e
e ![]() : allora l’equazione è IMPOSSIBILE perché non esiste nessun numero
: allora l’equazione è IMPOSSIBILE perché non esiste nessun numero ![]() che moltiplicato per zero genera un numero
che moltiplicato per zero genera un numero ![]() e ciò è confermato dall’impossibilità di dividere per zero in
e ciò è confermato dall’impossibilità di dividere per zero in ![]() .
.
Caso 2) ![]() e
e ![]() : allora l’equazione è INDETERMINATA perché qualunque numero
: allora l’equazione è INDETERMINATA perché qualunque numero ![]() che moltiplicato per zero il valore zero. In
che moltiplicato per zero il valore zero. In ![]() si ha la configurazione indeterminata zero diviso zero, cui non è possibile attribuire un valore univoco. Ricordate, zero diviso zero non viene uno! Si tratta di una forma indeterminata.
si ha la configurazione indeterminata zero diviso zero, cui non è possibile attribuire un valore univoco. Ricordate, zero diviso zero non viene uno! Si tratta di una forma indeterminata.
Caso 3) ![]() e
e ![]() : in questo ultimo caso ricadiamo nel caso generale, infatti si tratta di dividere il numero
: in questo ultimo caso ricadiamo nel caso generale, infatti si tratta di dividere il numero ![]() rispetto al numero
rispetto al numero ![]() , quindi nessuna difficoltà, viene
, quindi nessuna difficoltà, viene ![]() .
.
Che dite ci siamo? Direi di si. Abbiamo finito con la nostra introduzione alle equazioni di primo grado. Dobbiamo cominciare a guardare quelle di secondo grado. Teniamoci forte e partiamo.
Cominciamo col dire che una equazione di secondo grado ha una forma canonica del tipo:
![]()
Parecchio più difficile di quella di primo grado, ma niente paura, con alcune manipolazioni algebriche arriviamo al nostro obiettivo.
Cominciamo col dire subito, a differenza delle equazioni lineari dove ne abbiamo parlato in fondo, qualcosa sui coefficienti ![]() .
.
Se ![]() , oppure
, oppure ![]() , anche eventualmente assieme, sono uguali a zero non ci sono problemi, si ricasca nel caso generale che tratteremo tra poco.
, anche eventualmente assieme, sono uguali a zero non ci sono problemi, si ricasca nel caso generale che tratteremo tra poco.
Caso invece rilevante è se ![]() . Allora l’equazione di secondo grado si riconduce ad una di primo grado perché perde il termine che la caratterizza. Quindi si assume definitivamente che
. Allora l’equazione di secondo grado si riconduce ad una di primo grado perché perde il termine che la caratterizza. Quindi si assume definitivamente che ![]() . in tutto il resto del discorso.
. in tutto il resto del discorso.
Cominciamo ora le nostre trasformazioni algebriche che conducono al metodo per trovare i valori della incognita ![]() . Notate fin da ora che abbiamo detto “i valori” al plurale.
. Notate fin da ora che abbiamo detto “i valori” al plurale.
Data la ![]()
moltiplichiamo tutto il primo membro per il termine ![]() ottenendo
ottenendo ![]() che esplicitato conduce a
che esplicitato conduce a ![]() .
.
Sommiamo e sottraiamo dal primo membro la medesima quantità ![]() ottenendo
ottenendo ![]() .
.
Trasportiamo ora le ultime due quantità dal primo al secondo membro: ![]() facendo questa manovra hanno chiaramente cambiato di segno.
facendo questa manovra hanno chiaramente cambiato di segno.
Ora notiamo una cosa, i termini rimasti al primo membro sono un quadrato perfetto, in particolare il quadrato di ![]() , quindi
, quindi ![]() .
.
Siamo vicini, estraiamo la radice quadrata di entrambi i membri ottenendo:
![]()
Ecco comparire il segno ![]() che produce 2 soluzioni invece di una sola.
che produce 2 soluzioni invece di una sola.
A questo punto facciamo transitare l’addendo ![]() dal primo al secondo membro:
dal primo al secondo membro: ![]() e infine dividiamo entrambi i membri per
e infine dividiamo entrambi i membri per ![]() “scoprendo” la
“scoprendo” la ![]() ottenendo la formula definitiva:
ottenendo la formula definitiva:
![]()
Attenzione! Le soluzioni sono quindi 2, ma con una piccola difficoltà.
Vi ricordate la radice quadrata?
Noi la affrontiamo nell’insieme dei numeri reali ed in essi è necessario che il valore del numero sia positivo.
Nel nostro caso attribuiamo un nome alla quantità sotto radice: ![]() .
.
Dobbiamo farne la radice quadrata, che compare nella formula: ![]() e qui si possono presentare 3 casi: vediamoli.
e qui si possono presentare 3 casi: vediamoli.
Nel caso ![]() : in questo caso non è possibile calcolare la radice quadrata, di conseguenza non ci sono soluzioni reali neppure per l’equazione di secondo grado.
: in questo caso non è possibile calcolare la radice quadrata, di conseguenza non ci sono soluzioni reali neppure per l’equazione di secondo grado.
Caso ![]() : in questo caso la radice quadrata è anch’essa nulla, quindi le due soluzioni reali “collassano” sullo stesso valore.
: in questo caso la radice quadrata è anch’essa nulla, quindi le due soluzioni reali “collassano” sullo stesso valore.
Se ![]() : la radice quadrata è calcolabile generando un valore reale positivo, le due soluzioni reali sono tra loro distinte. (esempio rappresentato dal grafico).
: la radice quadrata è calcolabile generando un valore reale positivo, le due soluzioni reali sono tra loro distinte. (esempio rappresentato dal grafico).
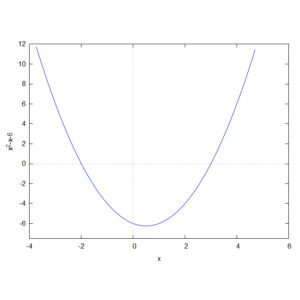
Le curve che rappresentano le equazioni di secondo grado si chiamano parabole.
Come si può vedere, è rappresentata una tra le tante possibili parabole, sono curve di nome e di fatto!
Dalla curvatura nascono le soluzioni che possono essere più di una.
Siamo alla fine, non è il caso di addentrasi oltre.
Solo una precisazione: abbiamo sempre aggiunto la parola reali alle soluzioni.
Perché?
La risposta è perché oltre ai numeri reali esistono anche dei numeri che consentono di calcolare la radice quadrata di numeri negativi. Ma la cosa è leggermente più complessa. Non a caso questi numeri sono detti numeri complessi.
Direi che abbiamo finito, spero vi sia piaciuto.
Al prossimo articolo.
Bye.

Commenti